
大家好!今天小师妹要向大家介绍一个在基因组学研究中非常重要的R包——SVA包!SVA(Surrogate Variable Analysis)包是一个专门用于校正基因表达数据中的批次效应和隐藏混杂因素的强大工具。随着RNA-seq和微阵列等高通量基因组技术的发展,如何减少非生物学因素对分析结果的影响变得至关重要,而SVA包恰好能帮助我们解决这个问题。它通过估计替代变量,有效去除技术因素对差异表达分析的干扰,显著提升分析的准确性。小师妹可是SVA包的忠实粉丝,如果大家有校正基因表达数据的困扰,随时可以联系我哦!
在本次学习中,我们不仅会学会如何安装和使用SVA包,还将掌握如何处理膀胱癌的基因表达数据、估计和校正混杂变量,以及结合limma包进行校正后的差异表达分析。通过实际示例的操作,我们将深入了解如何使用SVA包来消除批次效应,从而获得更可靠的研究结果。相信通过今天的学习,同学们能够更加熟练地应用SVA包,为自己的基因组学研究打下坚实的基础!接下来,请同学们跟紧小师妹的步伐,正式开启SVA包的学习之旅吧!
本次介绍的R包在服务器上能更加流畅地运行,如果没有服务器,欢迎联系我们进行服务器租赁~
sva包介绍
SVA(Surrogate Variable Analysis)包是R语言中用于校正基因表达数据中批次效应和隐藏混杂因素的工具。它通过估计未观测到的替代变量(Surrogate Variables),减少非生物学因素(如技术批次或实验条件)对分析结果的影响,从而提高差异表达分析的准确性。SVA 可以在未明确知道混杂因素的情况下有效调整数据,常用于RNA-seq、微阵列等高通量基因组学研究,帮助研究者避免假阳性结果,提高结果的可信度。
sva包安装
需要R语言版本为4.4,在控制台中输入以下命令:
if (!require(“BiocManager”, quietly = TRUE))
install.packages(“BiocManager”)
BiocManager::install(“sva”) #在BiocManager环境下安装sva包
查看是否安装成功:
packageVersion(“sva”) # 查看sva版本

显示为3.52.0版本,则表示已经安装了sva包。
除此之外,后续示例还需要使用bladderbatch, limma,这两个R包,我们可以提前安装,安装命令如下:
BiocManager::install(“bladderbatch”) # 在BiocManager环境下安装bladderbatch
BiocManager::install(“limma”) # 在BiocManager环境下安装limma
使用sva包校正高通量基因表达数据中的混杂效应。
载入需要的包和数据
首先,我们需要载入本次学习的主角——Bio3D包,以及其余两个需要用到的R包,相关代码如下:
library(sva)
# 加载 SVA 包,用于处理批次效应和估计替代变量。
library(bladderbatch)
# 加载 bladderbatch 数据包,其中包含膀胱癌的基因表达数据集。
library(limma)
# 加载 limma 包,用于差异表达分析中的线性模型拟合。
在本文中我们使用bladderbatch包中的膀胱癌相关数据作为示例,关注点是癌症状态的基因表达差异。载入数据的代码如下:
data(bladderdata)
# 从 bladderbatch 包中加载膀胱癌数据集 bladderdata。
bladderEset
# 查看bladderEset数据集的数据特征
显示结果如下图

由图可知,该数据集包含有57个样本的22283个数据特征。
提取表型数据并创建模型矩阵
在膀胱癌研究中,癌症状态是我们的主要关注点。数据存储在 ExpressionSet 对象中,该对象包含基因表达数据和样本的表型信息。
因此我们需要从 ExpressionSet 对象的表型数据槽中提取表型信息,并获取基因表达矩阵,代码如下:
pheno = pData(bladderEset)
# 从 bladderEset 对象中提取表型数据(样本信息),存储在 pheno 变量中。
edata = exprs(bladderEset)
# 从 bladderEset 对象中提取基因表达数据矩阵,存储在 edata 变量中。
随后我们需要使用提取到的数据创建模型矩阵,包括全模型和空模型。全模型:包含感兴趣的变量(癌症状态),癌症状态是多水平变量,因此用因子处理。空模型:仅包含截距,因为没有其他调整变量。
mod = model.matrix(~as.factor(cancer), data=pheno)
# 创建全模型矩阵
mod0 = model.matrix(~1, data=pheno)
# 创建空模型矩阵
使用 SVA 包估计替代变量
首先我们需要使用num.sv()函数来估计替代变量数量,代码如下:
n.sv = num.sv(edata, mod, method=”leek”)
# 使用 Leek 方法估计替代变量(surrogate variables, SV)的数量。这里是通过基因表达数据(edata)和全模型(mod)来确定的。
输出替代变量数量(n.sv),例如 n.sv = 2,表示有 2 个隐藏混杂因子。接着我们使用 sva()函数:评估替代变量。
svobj = sva(edata, mod, mod0, n.sv=n.sv)
# 使用 SVA 包中的 sva 函数来估计替代变量。输入的基因表达数据是 edata,全模型是 mod,空模型是 mod0,
校正后计算 F 检验 p 值
接下来我们使用f.pvalue()函数计算数据矩阵每一行的参数F来检验p值。F检验比较的是嵌套模型,因此mod和mod0中所有的变量都必须在mod中出现。首先,我们可以在不调整替代变量的情况下计算与癌症状态相关的差异表达的F检验p值,然后对它们进行多重检验校正,并计算在Q值小于0.05的情况下显著的基因数量。
不调整替代变量的 p 值:
pValues = f.pvalue(edata, mod, mod0)
# 使用 f.pvalue 函数计算 F 检验的 p 值。
qValues = p.adjust(pValues, method=”BH”)
# 使用 Benjamini-Hochberg (BH) 方法对 p 值进行多重检验校正,生成校正后的 q 值。
调整替代变量后的 p 值:在模型中加入替代变量。
modSv = cbind(mod, svobj$sv)
# 将估计的替代变量(svobj$sv)与全模型(mod)结合,创建一个包含校正替代变量的模型 modSv。
mod0Sv = cbind(mod0, svobj$sv)
# 同样地,将替代变量与空模型(mod0)结合,创建一个包含校正替代变量的空模型 mod0Sv。
pValuesSv = f.pvalue(edata, modSv, mod0Sv)
# 使用校正了替代变量的全模型和空模型计算新的 F 检验 p 值。
qValuesSv = p.adjust(pValuesSv, method=”BH”)
# 对校正混杂效应后计算的 p 值再次使用 Benjamini-Hochberg (BH) 方法进行多重检验校正,生成校正后的 q 值。
head(qValuesSv, n=20) # 查看矫正之后的q值结果
显示结果如下图:

结合limma包进行差异表达分析
limma 包是差异表达分析中最常用的包之一。sva 包可以很方便地与 limma 包结合使用,以执行校正后的差异表达分析。
这个过程的第一步是拟合包含替代变量的线性模型,代码如下:
fit = lmFit(edata, modSv) # 使用包含替代变量的模型矩阵 modSv 对表达数据 edata 进行线性拟合
随后,构建定义癌症状态之间的对比矩阵
contrast.matrix <- cbind(
“C1” = c(-1,1,0,rep(0,svobj$n.sv)), # 创建对比矩阵 C1,用于比较不同条件(例如条件1 vs 条件2)
“C2” = c(0,-1,1,rep(0,svobj$n.sv)), # 创建对比矩阵 C2,用于比较不同条件(例如条件2 vs 条件3)
“C3” = c(-1,0,1,rep(0,svobj$n.sv)) # 创建对比矩阵 C3,用于比较不同条件(例如条件1 vs 条件3)
)
fitContrasts = contrasts.fit(fit, contrast.matrix) # 应用对比矩阵进行差异表达分析,更新线性拟合模型
最后,使用 eBayes 计算检验统计量:
eb = eBayes(fitContrasts) # 使用贝叶斯方法来提高统计分析的稳定性
topTableF(eb, adjust=”BH”) # 输出 F 统计量的前几个结果,并使用 Benjamini-Hochberg 方法进行多重检验校正
显示结果如下图,
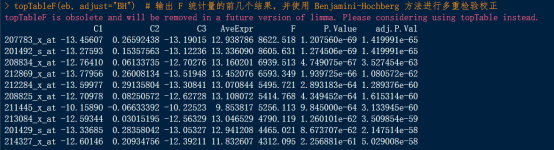
图中,207783_x_at 基因在 C1 对比下有 -13.45607 的 log2 fold change,C2 对比下有 0.26592438,而 C3 对比下为 -13.19015。这意味着该基因在不同条件之间存在较大的差异表达。其 F 统计量为 8622.518,原始 p 值极小(1.207560e-69),经过校正后的 p 值也是极小的(1.419991e-65),说明这个基因在这些条件下有非常显著的差异表达。
以上就是对SVA包的介绍。通过本文,我们了解了SVA包在校正基因表达数据中的混杂效应和批次效应方面的应用。SVA包通过估计替代变量来消除非生物学因素的影响,从而提高差异表达分析的准确性。同时,结合limma包可以进一步进行校正后的差异表达分析,准确识别出显著差异表达的基因。希望大家在学习和使用SVA包时,能够熟练掌握其基本操作,通过不断的实践和探索,在高通量基因组学研究中取得更大的进展和成果。
同学们如果觉得自己写代码麻烦,可以体验一下我们的云生信小工具,只需输入数据,即可轻松生成所需图表。立即访问云生信(http://www.biocloudservice.com/home.html),开启便捷的生信之旅!