2024-06-16

生信数据处理基础中的精华SVD：奇异值分解还能变成多维尺度变换？

小师妹生信果 2023-08-10 19:02:16

转自公众号：R语言学徒
http://mp.weixin.qq.com/s?__biz=Mzg5MDk3Mzg4OA==&mid=2247484878&idx=1&sn=3064578a2b93f8747b27757e7308069d

点击蓝字

关注我们

在生物信息学中，SVD奇异值分解是一种常用的矩阵分解技术，可以帮助进行数据降维。之前小师妹已经向大家介绍了SVD奇异值分解在降维中的应用。今天，小师妹将给大家带来SVD奇异值分解的另一项绝活——以SVD为基础的MDS多维尺度变换。MDS可以将高维数据点映射到一个低维空间中，以便更好地可视化和解释数据。我们将会使用和之前一样的组织基因数据集进行实例演示。通过使用SVD和MDS技术对数据进行降维分析，并可视化展示降维结果，可以更好地理解组织基因表达数据中的生物学信息。因此，SVD奇异值分解在生物信息学中是非常有用的工具，可以帮助我们更好地探索数据集的内在结构和模式。

MDS (Multi-Dimensional Scaling) 是一种经典的数据降维技术，旨在将高维数据映射到低维空间中，同时保留高维数据点之间的距离关系。MDS 的核心思想是将原始数据的相似性矩阵转化为低维空间中的距离矩阵，然后通过优化距离矩阵与原始相似性矩阵的差异来完成降维过程。

以SVD奇异值分解为基础的MDS技术则是用SVD奇异值分解的结果来计算降维后的距离。一般为了方便可视化，我们会尽量将特征压缩成二维。经过数学推导后我们可以知道高维样本i和j之间的距离近似于基于SVD降维后的二维点Z之间的距离。

那么现在我们就用例子直接看看如何应用吧！

第一步仍然是导入相关的工具包和我们的数据

library(rafalib)library(tissuesGeneExpression)data(tissuesGeneExpression)

这里我们为了简化，只保留肾、结肠、肝脏的组织信息

colind <- tissue%in%c("kidney","colon","liver")mat <- e[,colind]group <- factor(tissue[colind])dim(mat)   ##查看简化后的数据维度简化后的数据维度变为22215*99

接下来使用svd（）进行奇异值分解

s <- svd(mat-rowMeans(mat))

这里做了一个简单的预处理，通过减去每一列的均值（即 rowMeans(mat)），从而将数据矩阵的中心移到原点上。

在进行数据降维分析时，通常需要对原始数据进行预处理，以消除数据中的噪声、异常值或不必要的变量，并将数据转换为可用于降维分析的形式。在这种情况下，通过减去每一列的均值可以消除数据矩阵中的数据偏移，使降维分析更加准确和可靠。

计算出Z的坐标并对降维后不同组织的基因表达进行可视化

PC1 <- s$d[1]*s$v[,1]PC2 <- s$d[2]*s$v[,2]mypar(1,1)plot(PC1,PC2,pch=21,bg=as.numeric(group))legend("bottomright",levels(group),col=seq(along=levels(group)),pch=15,cex=1.5)

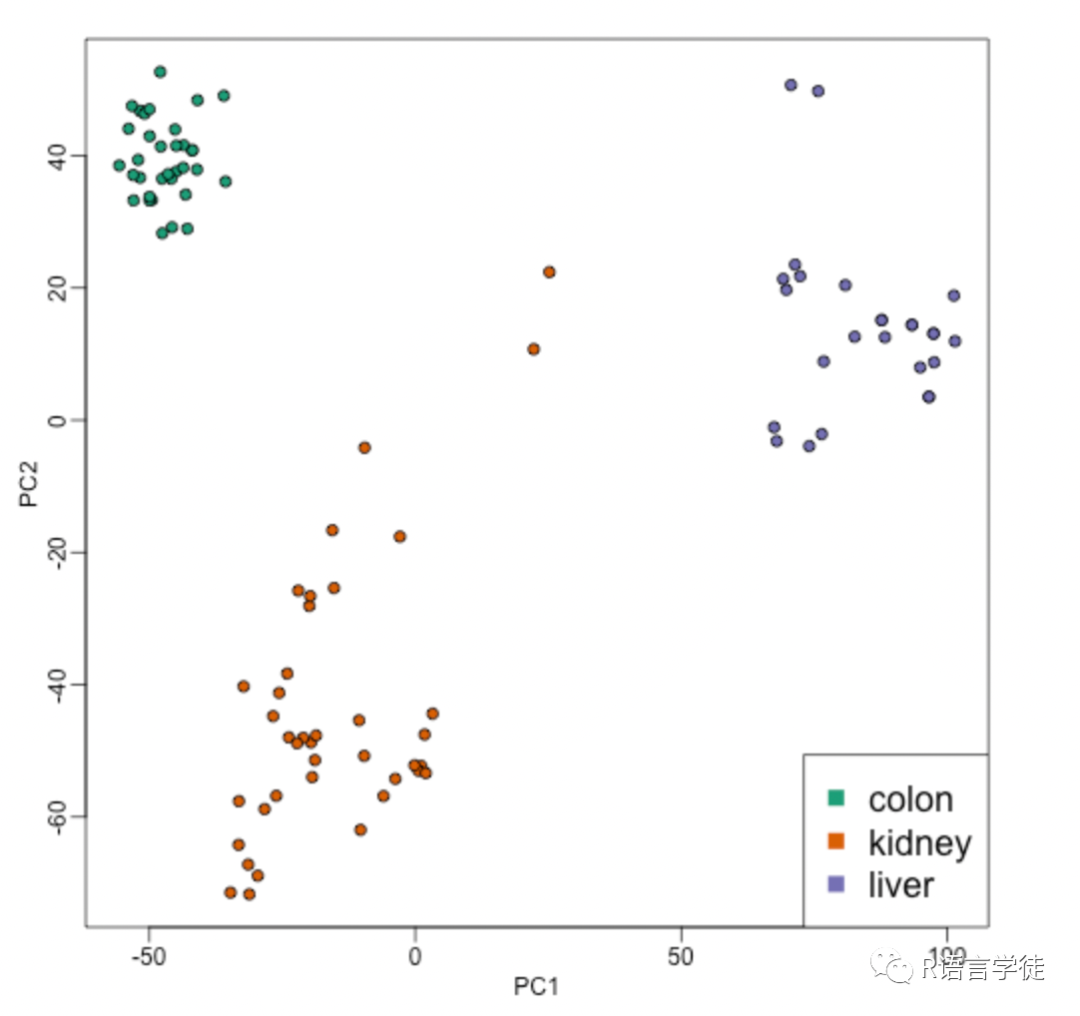
我们可以看到，通过提取前两个奇异值来计算每个数据点的距离，将数据压缩到二维空间之后，不同类别的三类组织基因数据点仍然可以得到很好的区分。

上述近似的准确性取决于前两个奇异值解释的方差的比例。

如上所示，我们可以通过绘制方差解释图来快速看到这一点:

plot(s$d^2/sum(s$d^2))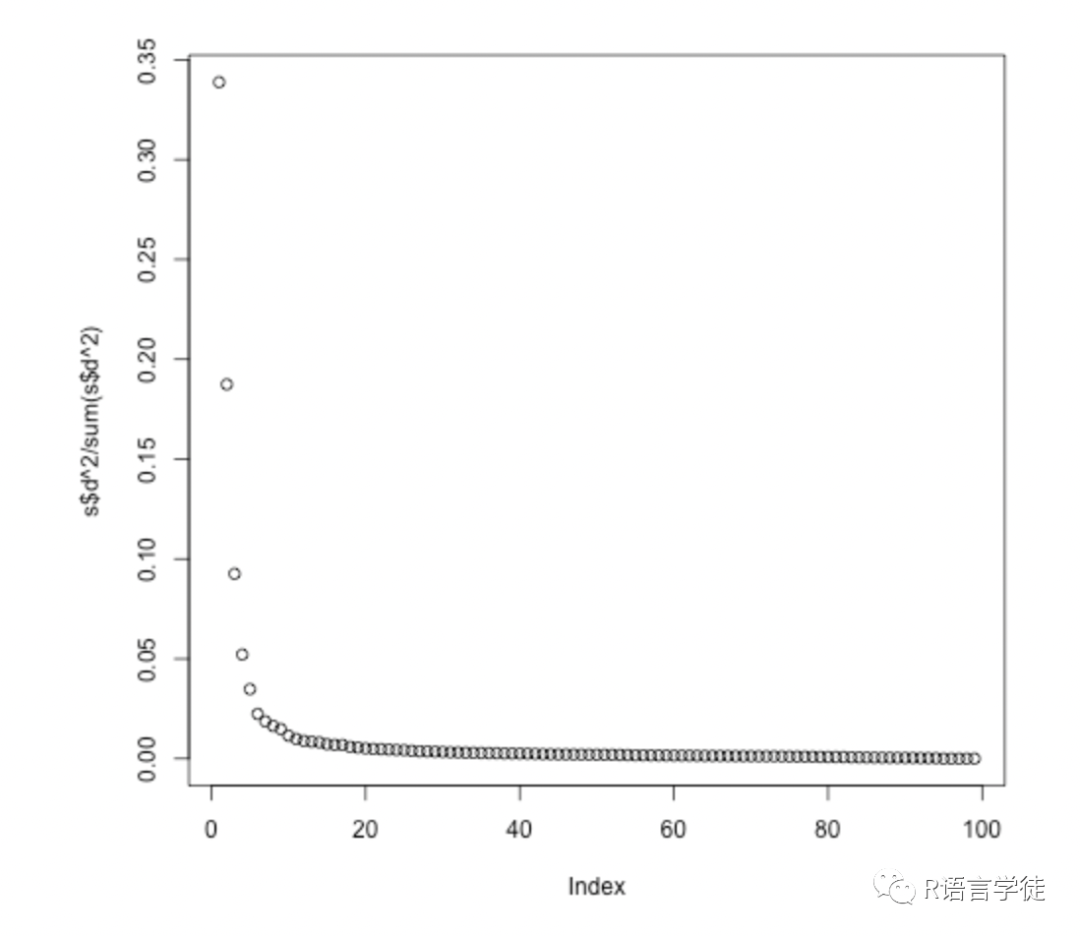

这里我们可以看到前两个奇异值解释了50%以上的变化。但是通过这个图，我们还可以发现的是，第三、第四个奇异值也能解释不少的信息。

那么我们现在就来看看第三、第四个奇异值的情况吧～

PC3 <- s$d[3]*s$v[,3]PC4 <- s$d[4]*s$v[,4]mypar(1,1)plot(PC3,PC4,pch=21,bg=as.numeric(group))legend("bottomright",levels(group),col=seq(along=levels(group)),pch=15,cex=1.5)

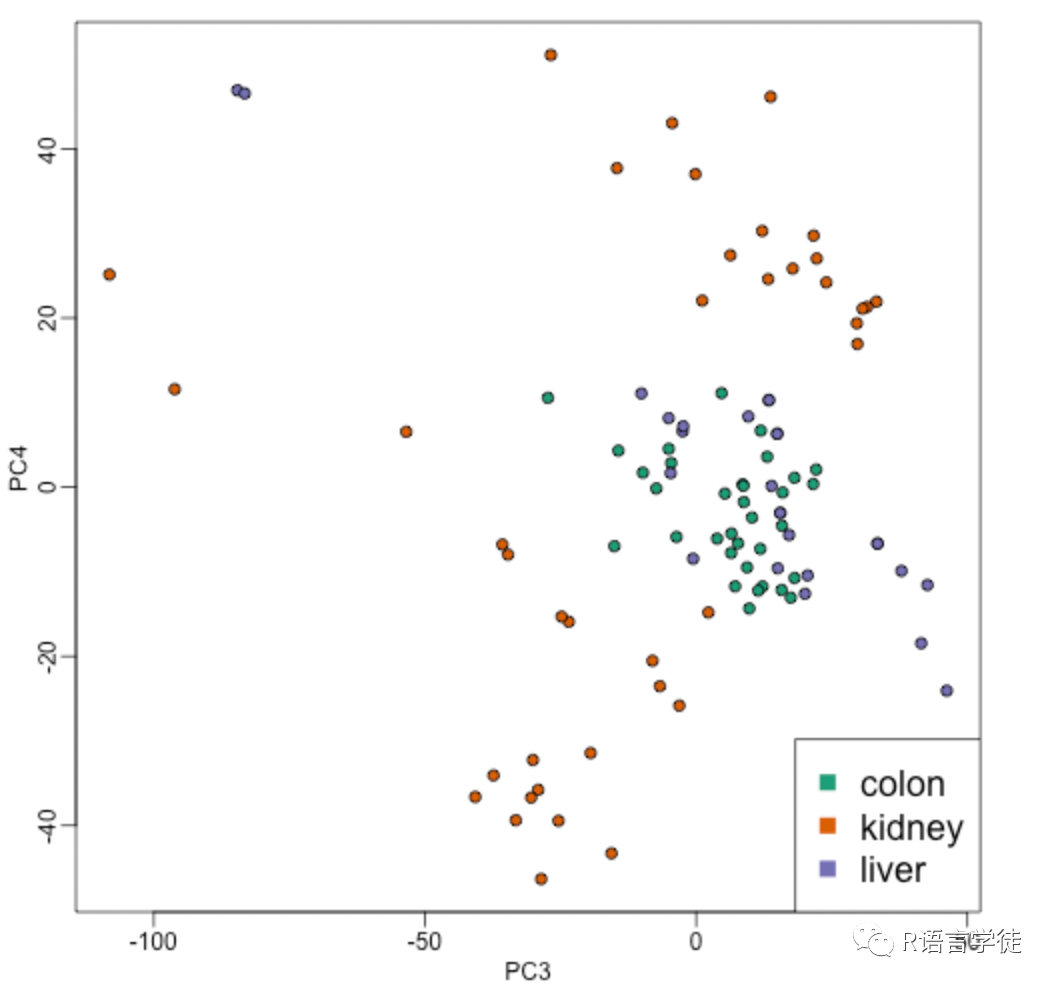
这里我们可以看到，使用第三、第四个奇异值降维后，三类组织的分类效果确实不如第一、第二个奇异值。但是值得注意的是，肾的组织可以得到很好的分离（橙色的点）。

虽然我们使用了上面的svd函数，但是对于MDS多维尺度变换有一个专门设计的特殊函数cmdscale（）。它将距离对象作为参数，然后使用主成分分析来提供用k可以获得的距离的最佳近似值维度。

d <- dist(t(mat))mds <- cmdscale(d)
mypar()plot(mds[,1],mds[,2],bg=as.numeric(group),pch=21,xlab="First dimension",ylab="Second dimension")legend("bottomleft",levels(group),col=seq(along=levels(group)),pch=15)